Beispiel: hier wird ein 30-Eck aufgeteilt in ein Sechseck, Fünfeck, Zehneck und Dreieck entsprechend der möglichen Teiler von 30 (30=5*6; 30= 2*15; 30 =3*10; ).
Geometrie
1. Ausgangspunkt
Meine geometrischen Muster bestehen aus regulären Polygonen (Polygonen mit gleicher Seitenlänge und gleichem Innenwinkel). Solche Polygone sollen aneinandergereiht werden, so daß die Ebene ohne Überlappung und Restfläche bedeckt ist. Dieser Forderung entsprechen nur eine bestimmte Anzahl an Polygonkombinationen, die, soweit nur konvexe Polygone herangezogen werden, bekannt sind:
Als lokale Regel, die eine Anlagerung an einem Eckpunkt vornimmt ohne auf Fortsetzbarkeit Rücksicht zu nehmen, kann die Folgende gesehen werden: Das zentrale Polygon (n-Gon, n= 360°/ a) wird Objekt der Anlagerung.
1. Anlagerung kompletter konvexer Polygone:
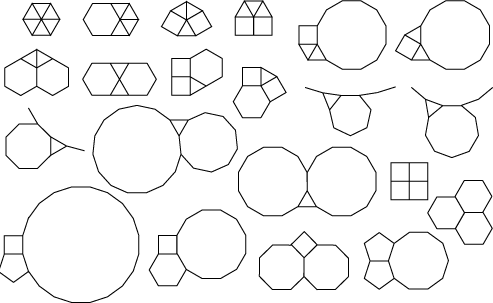
An ein ausgangs festgelegtes n-Gon werden zwei bis fünf (maximale Anzahl bei regulären Dreiecken) n-Gons angelagert. Dabei gilt, daß die Winkelsumme an einem Eckpunkt, an welchen die regulären Polygone zusammenkommen, exakt 360° ist. Aus dieser Forderung ergeben sich die oben aufgelisteten Möglichkeiten. Algorithmisch habe ich dies in einer vorläufigen Softwareso gelöst, daß ein Array aller Innenwinkel in einer Doppelschleife inkrementiert wird, wobei jeweils zwei Innenwinkel verschiedener Polygone addiert werden. Ist die Winkelsumme mit dem Ausgangspolygon 360° exakt, wird die Lösung angezeit.
Sollen jedoch auch Polygonsterne (hier auch konkave Polygone genannt) herangezogen werden, ergeben sich eine Vielzahl von Möglichkeiten, die auch in der Literatur noch nicht alle bekannt sind.
Aus diesem Grund, aber auch dem Wunsch, neue und komplexe Muster zu finden, soll die Anlagerung als lokale Regel gefunden werden, die jeweils an einem Eckpunkt eines Polygons ansetzen kann. Dies kann geschehen, indem Koordinalten der Eckpunkte mit Aussenwinkel und Seitenlängen gespeichert werden, des weiteren mögliche bereits angelagerte Polygone und ihrer Drehung im Koordinatensystem (als Funktion). AIle sich ergebenden Fernwirkungen (Bedingungen für andere Eckpunkte) müssen weitergereicht werden an diese.
Im Folgenden möchte ich vorzunehmende Anlagerungen durchexerzieren. Sie könnten als Funktionen abrufbar sein.
Konstruktionselemente
2.1.Mustergenerierung durch Anlagerung von Polygonsternen
Fügt man dem Formenkanon Polygonsterne hinzu, so wird das Spektrum der Anlagerungen erheblich erweitert. Zunächst sei festgelegt, daß Polygonsterne gleiche Seitenlängen haben und zwei verschiedene Winkel an ihrer Aussenseite (den Winkel an der Spitze und der an der Einbuchtung). An der Einbuchtung können generell auch mehrere Winkel sein, sie sollten (müssen aber auch nicht) zu einer Achse von der Spitze des Sterns zu seinem Mittelpunkt symmetrisch sein.
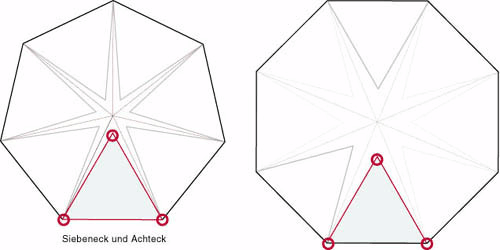
Betrachten wir zuerst Sterne mit je einer Spitze und einer Einbuchtung: Für Parkettierungen machen natürlich nur solche Sterne Sinn, die sich mit regulären Polygonen verbinden. Dabei sei zunächst der Fall zu betrachten, daß ein reguläres Polygon drei Eckpunkte mit dem Stern teilt. Für ein Dreieck ist der kleinste, passende Stern ein Siebenstern. Man beachte, daß für das Dreieck dann in den Folgeanlagerungen dieselben Reglen gelten wie die für ein n-Gon der Symmetrie des Sterns. Bereits beim Viereck ergibt sich als Gesammtform ein Stern.
Im Folgenden die Anlagerung an ein Fünf- und einen Sechsstern. Die Erhöhung der Symmetrie kann beliebig fortgesetzt werden. Die Anzahl der außenliegenden Ecken, die für die Anlagerung relevant werden, beträgt Sternsymmetrie * (Polygonsymmetrie -2). An den Ecken liegen zwei Winkel vor, die sich wie folgt berechnen:
1. Winkel an der Spitze des Stern:
(a sei die Symmetrie des Polygons, b die Symmetrie des Sterns) 360° -(360°-180°-(360°/a) - 360°/b
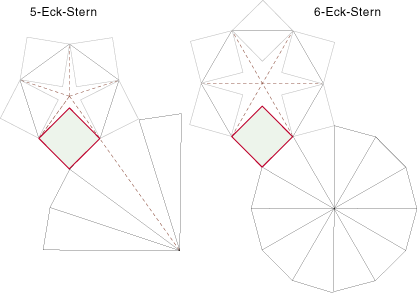
2. Winkel am Polygon:180°-(360°/a)
Der Algorithmus ergibt sich, indem man durchrechnet, für welche Polygonaußenwinkel (2 Stück) plus Winkel an der Spitze des Sterns sich ein passendes N-Gon findet (Bedingung: Außenwinkel = 180°- (360°/n), wenn n eine ganze Zahl ist.
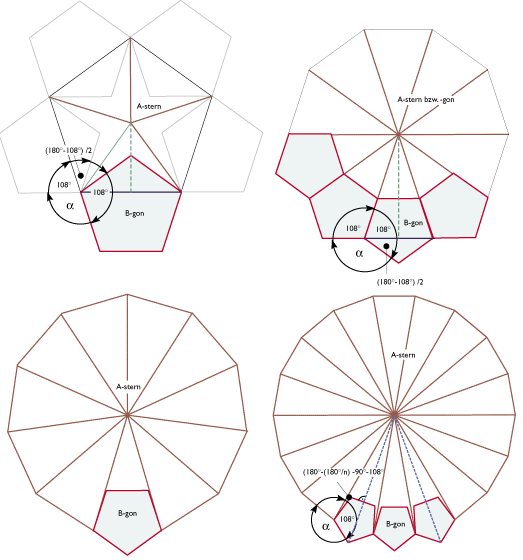
Nun sei der Fall betrachtet, daß beide mehr als drei Punkte gemeinsam haben.
Welche Winkel ergeben sich für die Anlagerung an einen solchen Stern?
1. a berechnet sich aus dem Winkel an der Spitze + 2* Innenwinke des B-gons (180°- (360°/b)).
2.1 Der Winkel der Sternspitze ergibt sich im Falle dreier gemeinsamer Eckpunkte:
(360°-(360°- (180°-(360°/B))- 360°/A)/2 = g
2.2 Im Falle vier gemeinsamer Eckpunkte berechnet sich die Sternspitze aus
360° - (360°- (180°-(360°/B)) - (360°/ A) - 90° = g
Der Algorithmus ergibt sich genauso wie oben, aus der Berechnung möglicher Anlagerunspolygone, die den Außenwinkel haben 360° - (2 * B-gon-Außenwinkel) - A-gon-Spitze.
Findet sich durch die "Umgebung" des Anlagerungsort keine Lösungen, kann auch ein Stern aus zwei oder mehrerer nebeneinander liegender Polygone gebildet werden.Im Folgenden die illustrierte Konstuktionsvorschrift:
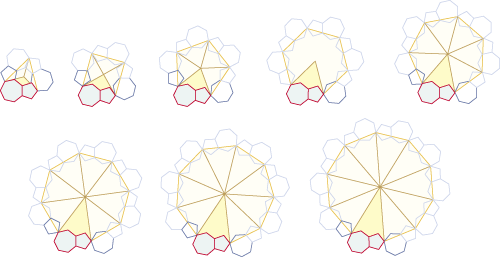
2.2. Beschnittene Polygone als Anlagerungselement
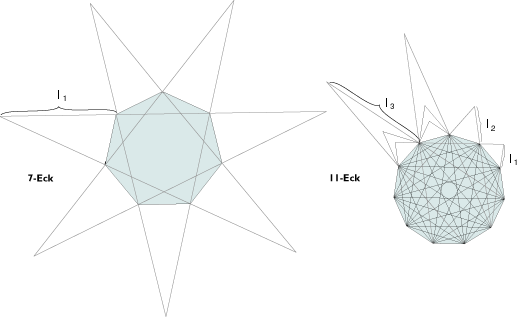
In den seltensten Fällen nur ist es möglich, an eine erste Generation von angelagerten regulären Polygonen eine zweite "Generation" von Polygonen anzulagern. Gelingt dies nicht, so ist erlaubt, wie im vorigen Procedere gezeigt, Polygonsterne einzubinden. Ist die Konstruktionsvorschift nicht eindeutig aus einer Umgebundg abzuleiten, dann seien die im Folgenden dargestellten zu bevorzugenden Möglichkeiten der Polygonsternbildung einzusetzent:
für l1 in Abhängigkeit von s (Aussenseite des Polygons) und a (360° / Anzahl der Ecken des Polygons) gilt:
l1=s /2*cos(a+ a/2)
l2=s /2*cos(a+ 2*a/2)
l3=s /2*cos(a+ 3*a/2)
...
ln=s /2*cos(a+ n*a/2)
Weisen also zwei benachbarte Seiten ein Verhältnis wie s/ln auf und ist der Winkel *(a+ n *a/2),so bietet sich die Bildung des Sternes an. (wenn der Winkel >a+ n *a/2 ist, muss der Restwinkel anderweitig auffüllbar sein, z.B. durch den Innenwinkel eines Polygons). Die Formulierung als Algorythmus verlangt die Speicherung von Winkel und Längenverhältnis als einer Anlagerungseinheit, die es zu testen gilt.
Ist es nicht möglich, solche Sterne oder eine einzelne Sternzacke einzufügen, soll auch möglich sein, ein Polygonausschnitt als Anfügeelement auszuwählen, insbesondere, wenn dadurch eine Fläche zu einem weiteren kompletten Polygon überbrückt wird.
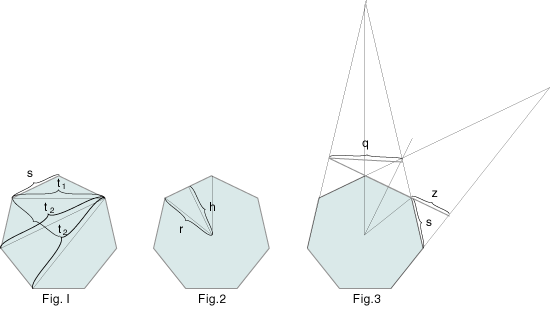
t steht hier für den Schnitt durch zwei nicht nebeneinanderliegende Punkte eines Polygons (Fig. 1).
Es seinen auch Schnitte durch den Mittelpunkt des Polygons erlaubt.
Die kleinste Operationseinheit sei ein rechtwinkliges Dreieck mit Winkel a/2 und (180 -a)/2 (FIg. 2). Dieses kann um
t1= 2* s cos ( a/2) 360°-(180°-a) - 4a
t2=s + 2* s cos ( 2* a/2)
t3=t1 + 2* s cos ( 3* a/2)
(360°/a)-1 * a gedreht werden und ebensooft abgebildet weden. h berechnet sich als cos (a/2 ) aus r. Der einfachste Stern ist der, der durch Verlängerung der Seiten des Polygons entsteht (Fig. 3). die Seite z errechnet sich als z= s/(2*cos a).
3.1.Anlagerungsmodus
Generell gibt es zwei Arbeitswege:
ad 2.
Häufiger sind die Fälle, in welchen ein beliebiges Polygon oder Polygon plus Sternspitze einen Winkel bilden, zu dem man eine Sternanlagerung sucht. Bedingung ist dann meist, daß der einzufügende Winkel Sternspitze plus Polygonaussenwinkel beträgt. Als Algorithmus wird dann gerechnet, ob bei einem entsprechenden Winkel p ein Winkel r besteht, der Bedingung ist für eine Stern.
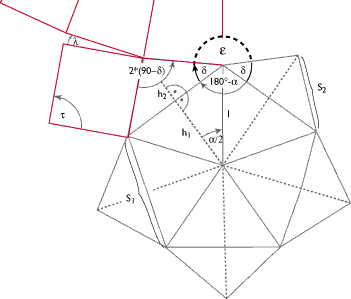
An das n-Gon werden Polygonsterne und Polygone angelagert nach der unten beschriebenen Art:
Ein Ausgangspolygon (mit der Symmetrie 360°/a) hat Spitzen (Sternzacken), die um den Winkel d das konvexe Polygon überschreiten. Hier kann d in Abhängigkeit von e gewählt werden. Für e gilt, daß er entweder
Dies bedeuted,
d ist zu finden entweder
1.1 in Abhängikeit von einem regulären n-Gon, dessen Außenwinkel e entspricht (d= (360° - e - 180° - a)/2)
1.2 in Abhängikeit von mehreren regulären n-Gons, deren Außenwinkel e entsprechen (d= (360° - e1 -e2 ... - 180° - a) /2)
2. e so zu wählen ist, daß entweder ein l vorhanden ist, das mit einem n-gon mit Aussenwinkel t ein Sternmuster bildet (Bedingung: 360° / n = ( 360° - t ) + 2 * l, wobei n eine ganze Zahl ist) oder e so zu wählen ist daß 360° - a - e gleich dem Außenwinkel eines regulären Polygons ist.
3.2.Anlagerung mit Unterteilung
Werden nach der oben beschriebenen Weise keine fortsetzbaren Lösungen gefunden, dann kommt folgendes Verfahren zum Einsatz:
Ein reguläres n-Gon wird unterteilt:

Beispiel: hier wird ein 30-Eck aufgeteilt in ein Sechseck, Fünfeck, Zehneck und Dreieck entsprechend der möglichen Teiler von 30 (30=5*6; 30= 2*15; 30 =3*10; ).
Die entstehenden 1/6, 1/5, 1/3, 1/15, 1/10 tel des Polygons werden wiederum unterteilt, um Anlagerungen ohne Überlappungen und Restflächen zu ermöglichen.
Beispiel: 30 - Eck mit angelagertem Viereck (C) und eingerücktem Neuneck (B) an 5/30tel eines 30 - Ecks
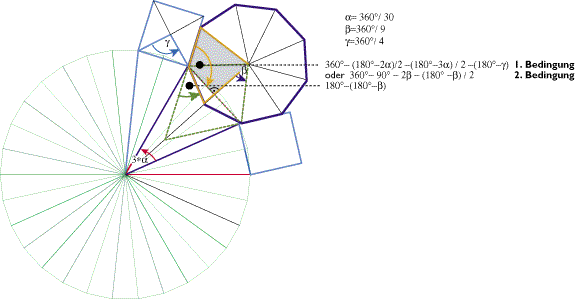
Das einzurückende Polygon (dunkelblau, hier Neuneck) berechnet sich nach Festlegung von a und dem Teiler aus Bedingung 1 und 2. Wird a festgelegt, dann ist b zu errechnen und umgekehrt. Der Algorithmus kann wieder unter Zuhilfenahme des Arrays von Außenwinkeln geschrieben werden (alle möglichen Außenwinkel werden ausprobiert, stimmt die Winkelsumme, dann ist eine Lösung gefunden). (Bedingung: t = 180°-360°/n und t = 360° - e - t ).
3. in Abhängigkeit von einer Sternspitze mit Winkel f und zweier Außenwinkel e1 , die zusammen e ergeben. Ist S2 größer als S1, dann gilt für t: t= 360°- e - (2*90-d).
1. Version der Anlagerung:
Die Wahl der (hier blau gezeichneten) anzulagernden Polygone mit den Winkeln am Mittelpunkt b und g ist in Abhängigkeit von a zu wählen.
Die Innenwinkel von 3/30-tel und 2/30-tel des zentralen Polygons sind als Summe immer gleich, egal ob die 5/30-tel in 1 und 4 oder 2 und 3 aufgeteilt werden. Für die Berechnung der anzulagernden Polygone ist also erst a und der angewandte Teiler (hier 5 ) ausschlaggebend.
Für die Summe der Innenwinkel des B-Gons und C-Gons gilt also
180°- b + 180°- g = 360°- (360°- 5a - (180°- 2a )/2 -(180° - 3a )/2)
Der Algorithmus für die Berechnung kann also über Inkrementieren von b und g als Werte eines Arrays, in welchem alle möglichen Innenwinkel eines regulären Polygons niedergelegt sind, formuliert werden.
4. Geometrische Beschreibung des Abstands zweier beliebiger regulärer Polygone
Idee des Programmes ist, Netzwerke aus Polygonen zu erzeugen. Diese Netzwerke sollen jedoch Bezug nehmen auf eine konkrete Situation, die Anhaltspunkte liefert für geometrische Strukturen (Bewegungsbahnen, Luftfotos).
Deshalb soll das Programm auch so angelegt werden, daß beliebige voneinander entfernte Polygone aufeinander Bezug nehmen können (der Bezug geometrisch beschrieben werden soll). Im Folgenden werden die Verfahren aufgezeigt, mit welchen dies zu erreichen sein wird.
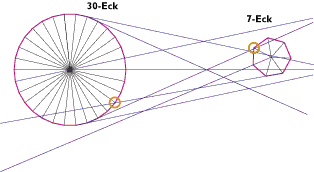
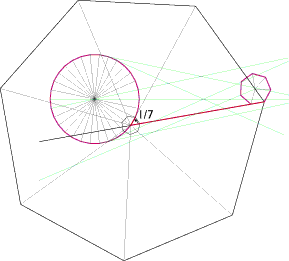
1. Alle Seiten beider Polygone werden verlängert zu Geraden. Alle Eckpunkte eines Polygons werden mit dem Mittelpunkt desselben verbunden. Es wird ermittelt, ob eine diese Geraden auf jeweils einem Eck- oder Mittelpunkt von beiden Polygonen liegt.
Beispiel (Zeichnung oben): Da der Schnittpunkt 2 offensichtlich eine kleinere Fehlertoleranz hat, wird dieser auf Winkel und Distanzen hin untersucht. Hier wurde der Winkel der betreffenden Geraden als 1/7 eines Kreises zur Außenseite des 30-Eck gefunden. Die rote Linie gibt die zu den Polygonen gehörigen Geraden an.
Im nächsten Schritt geht es darum, die Längenverhältnisse der Linien aufeinander zu beziehen. Hierzu wird zuerst das zu dem gefundenen Winkel gehörige Polygon gezeichnet, beispielsweise durch einen Eckpunkt des zweiten Polygons.
Dann geht es darum, 30-Eck und Siebeneck (großes, neugezeichnetes) wieder miteinander zu verbinden. Das soll durch Polygonanlagerung erfolgen, wie sie oben beschrieben wurde.Hier kann jedoch nicht allein von Winkeln ausgegangen werden.
2. Werden keine Schnittpunkte gefunden, so wird ein Kreis konstruiert, auf dessen Linie drei Punkte der beiden Polygone liegen, wobei der Mittelpunkt dieses Kreises nicht der Mittelpunkt der Polygone sein soll (oder anderst gesagt: ein Punkt muß mindestens auf dem zweiten Polygon liegen).
als Beispiel folgende Zeichnungen, bei denen zu den farbig markierten Eckpunkten jeweils die Kreise gefunden wurden.
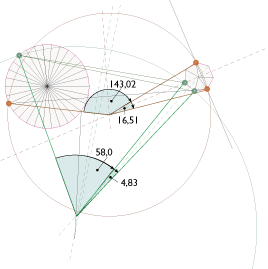
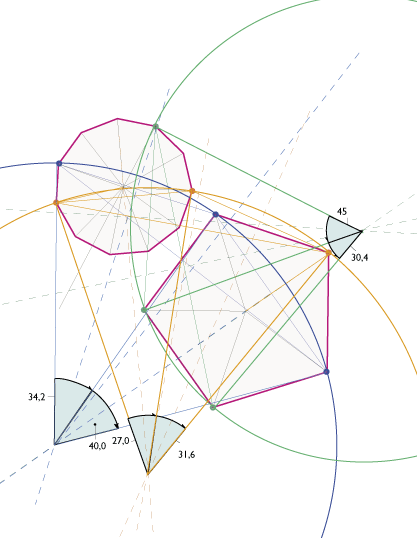
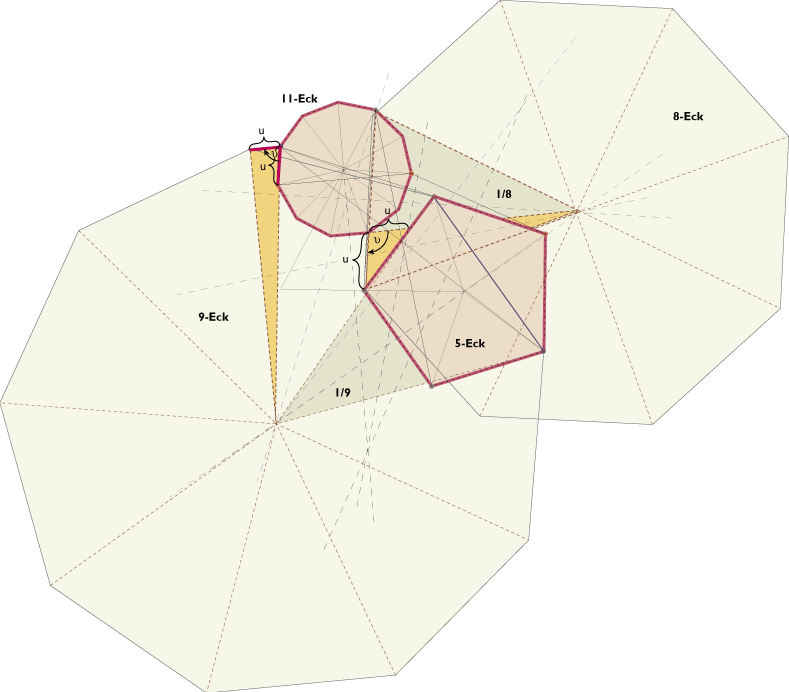
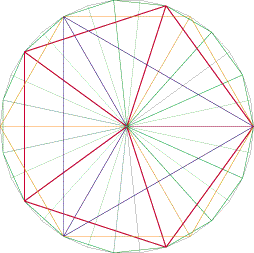
Dies geschah, indem für die beiden Punkte, die auf einem Polygon liegen, die Gerade konstruiert wird, auf welcher alle Punkte gleichen Abstands zu diesen Punkten liegen. dasselbe geschah für einen dieser Punkte und dem Punkt auf dem anderen Polygon. Der Schnittpunkt dieser Geraden wurde zum Mittelpunkt des Kreises. Nun werden die Winkel untersucht, die die Strecken zueinander bilden, die den Mittelpunkt des Kreises mit den ausgewählten Eckpunkten verbinden. Ist einer dieser Winkel 360°/ Z (Z steht für eine ganze Zahl größer als 2) oder ein Vielfaches davon, dann wird der Kreis zum Kreis um ein regulärens Polygons, dessen Symmetrie Z ist. Ausgehen von diesem Polygon werden weitere Anlagerungen nach dem vorne beschriebenen Prinzip gesucht. In Beispiel 1 ist keiner der Winkel ein möglicher Winkel eines regulären Polygons (360°/3, 360°/4, 360°/5 etc.) In Beispiel 2 allerdings gibt es gleich zwei Möglichkeiten: einen Winkel zu 40° (9-Eck) und einen zu 45° (8-Eck).
Testet man nun die jeweils drei auf einem Polygon liegenden Punkte, so wird ersichtlich, daß zwar eine integration beider Elemente in ein symmetrisches Raster des konstruierten Polygons möglich ist, die Weiterführung jedoch deshalb schwer, weil es jeweils Zwischenraäume zwischen den entsehenden Polygonen zu füllen gibt, die beliebig sind (unten rot markiert).
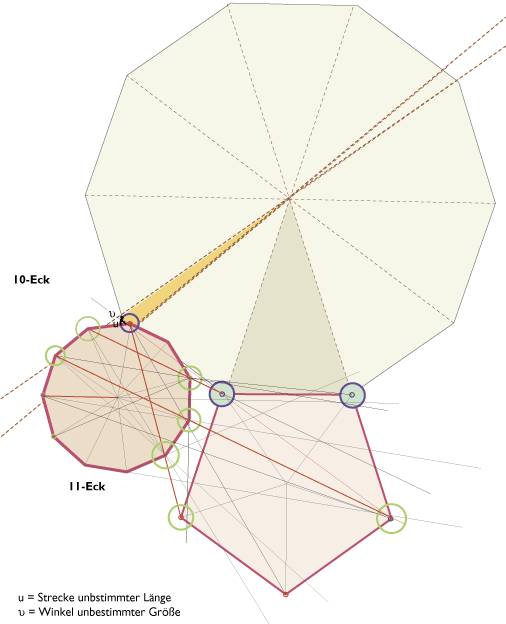
Es scheint deshalb ratsam, jeweils vier Punkte, also zwei Strecken von Polygonen aufeinander zu beziehen. Diese hier gezeigt Methode ist nur möglich, wenn das Programm keine Lösungen für Bezugnahme zweier Linien zeigt.